Раскраска Графа (37 Фото)

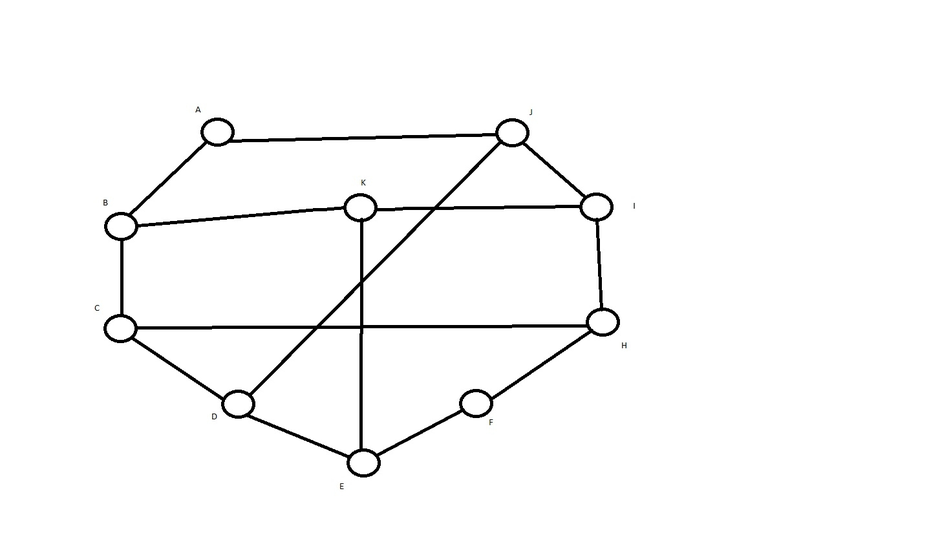
Раздел дискретной математики, изучающий графы. В самом общем смысле граф - это множество точек, которые соединяются множеством линий.

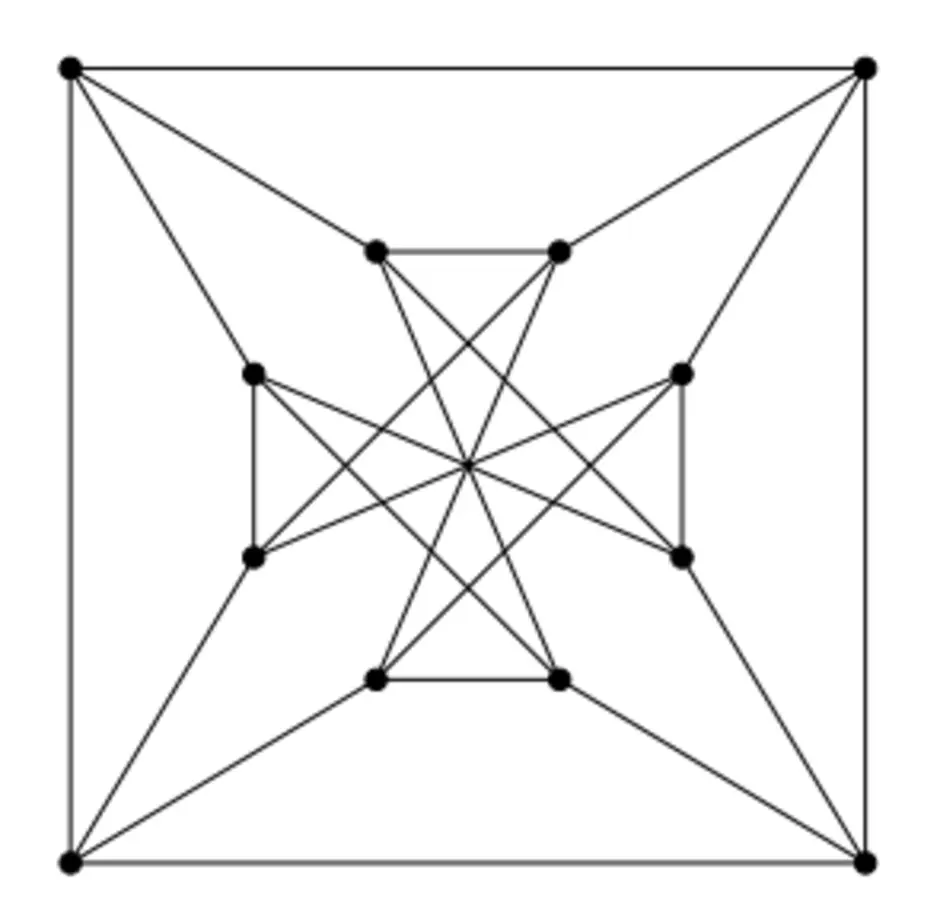
Неориентированный граф с 10 вершинами и 15 рёбрами; достаточно простой граф, используемый в качестве примера и контрпримера для многих задач в теории графов. Назван в честь Юлиуса Петерсена, построившего его в 1898 году как наименьший кубический граф без мостов, не имеющий рёберной раскраски в три цвета.

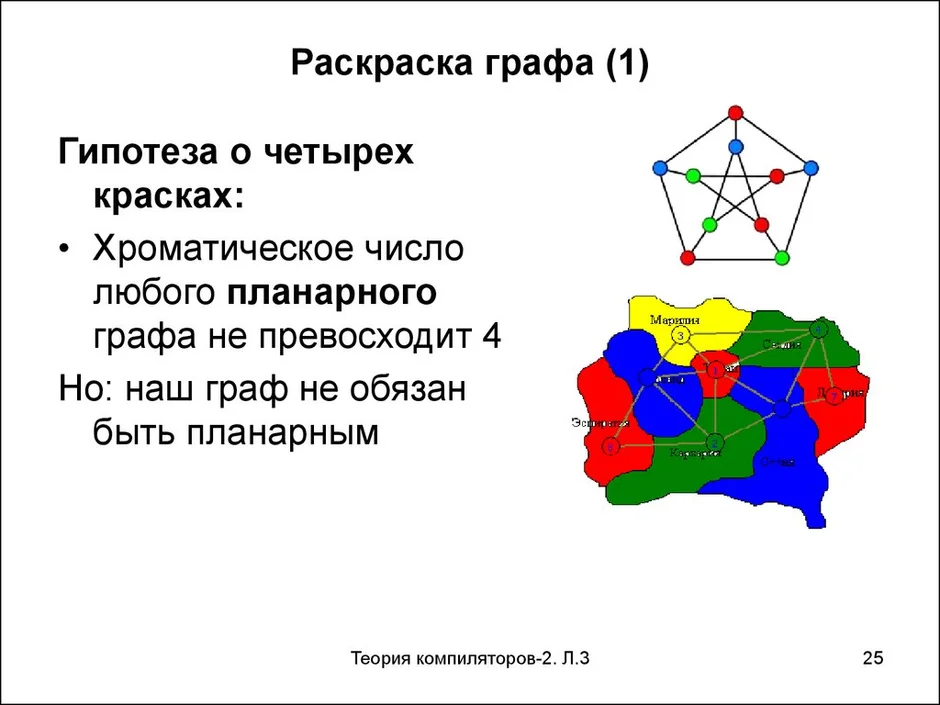
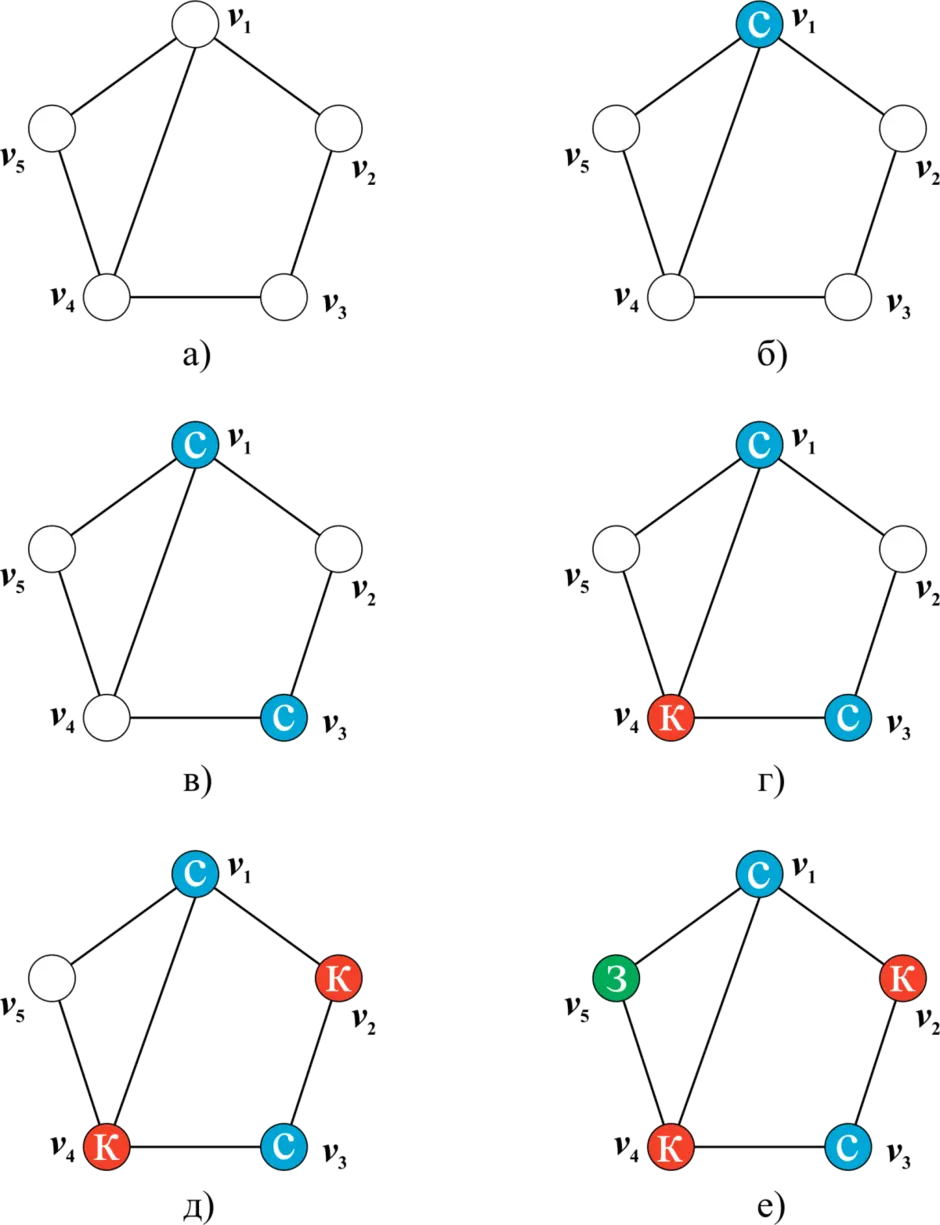
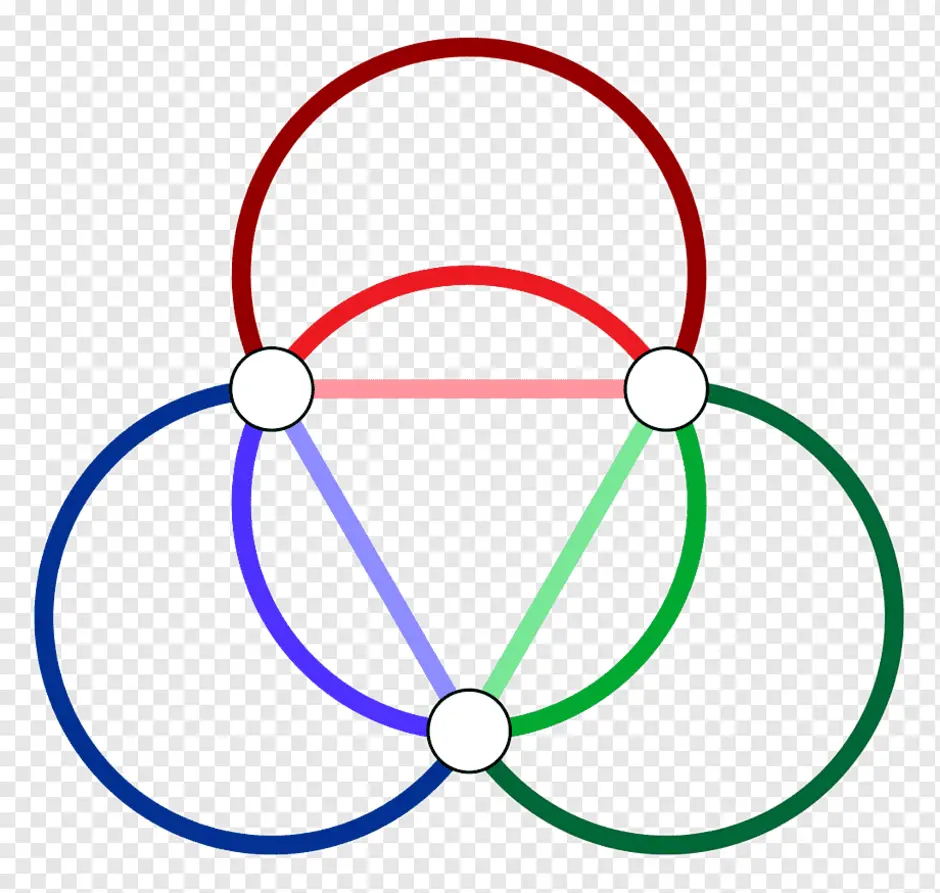
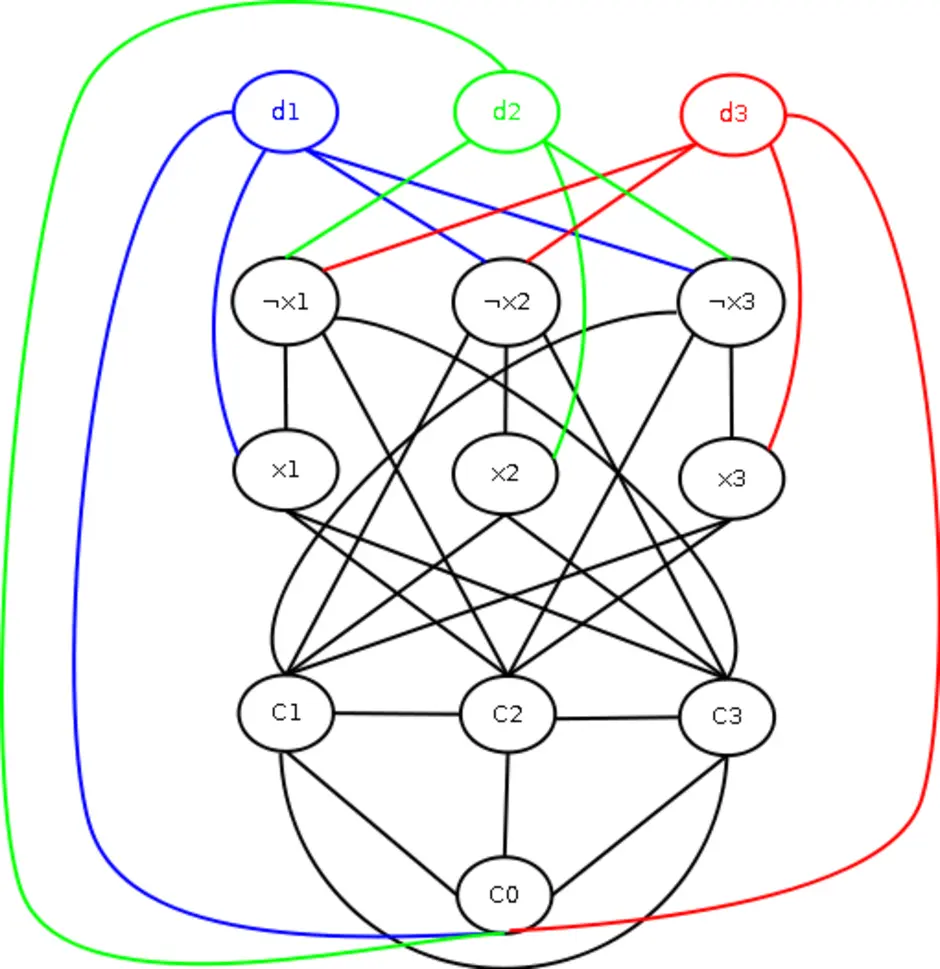
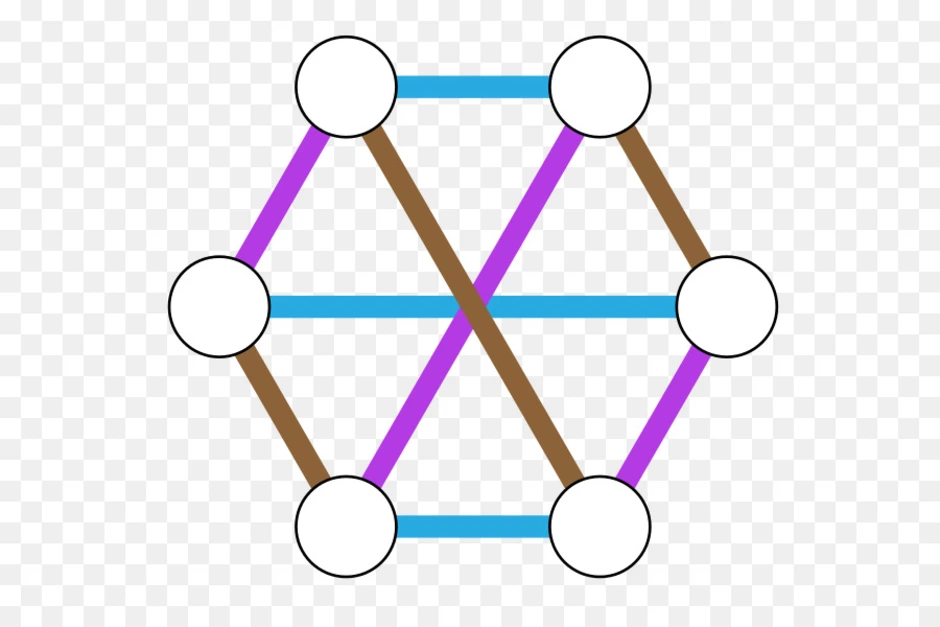
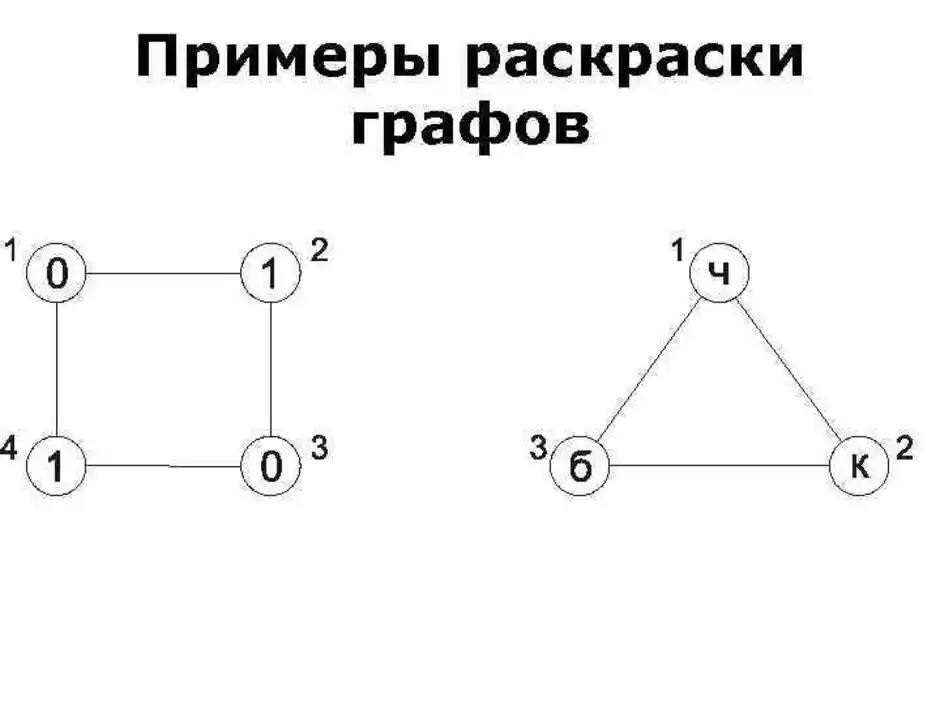
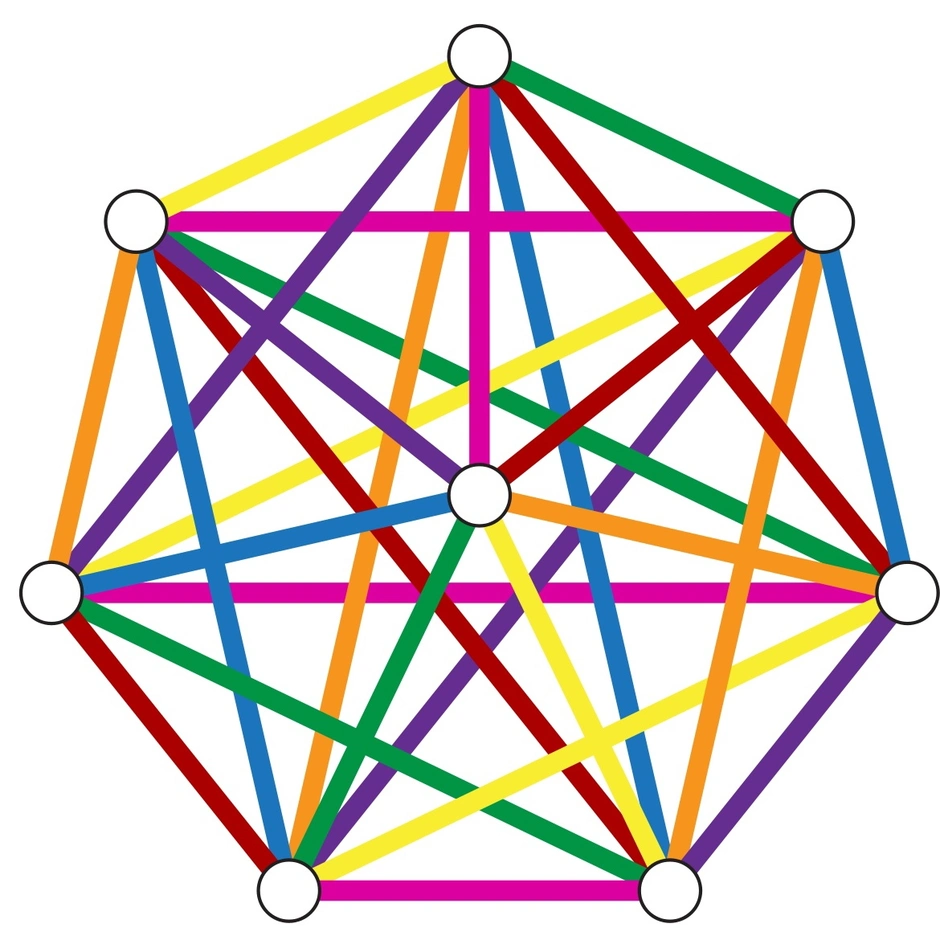
Теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин. Аналогично раскраска рёбер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета. Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.

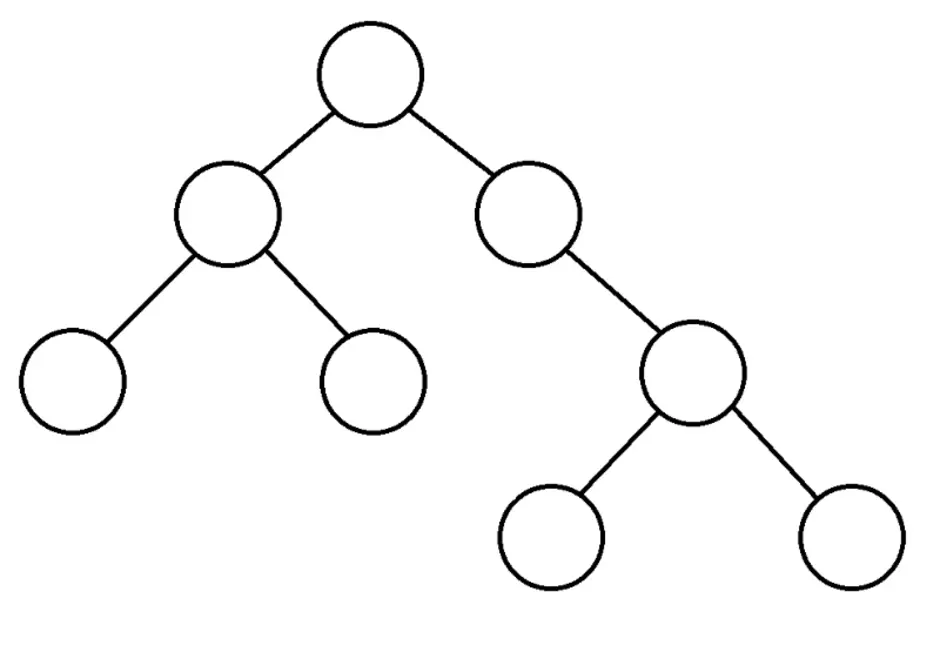
Иерархическая структура данных, в которой каждый узел имеет не более двух потомков. Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. Двоичное дерево является упорядоченным ориентированным деревом.

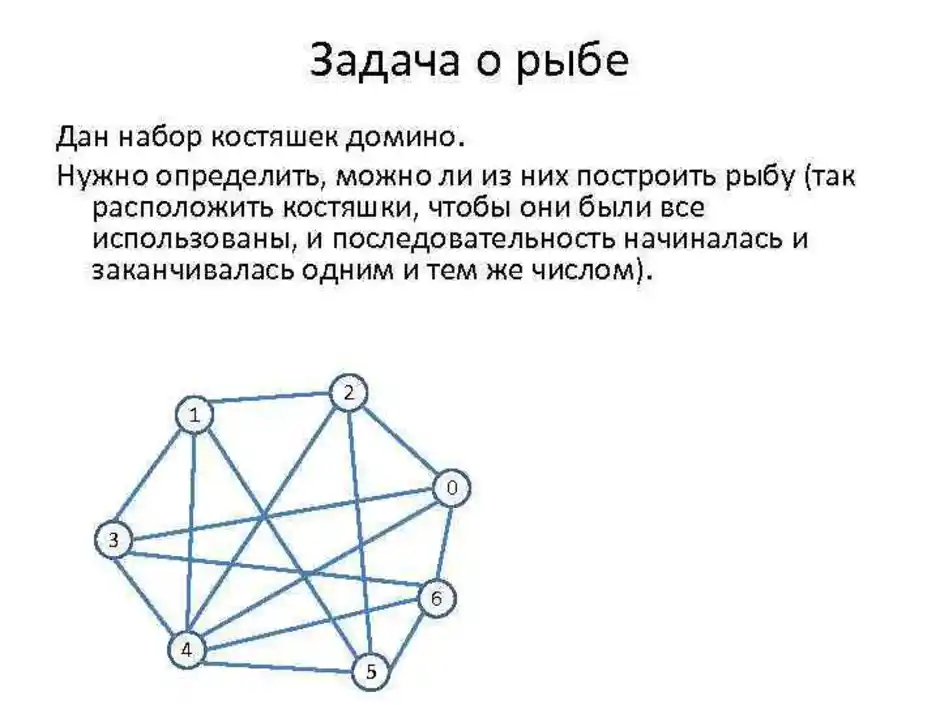
Специальный вид двудольного графа, у которого любая вершина первой доли соединена со всеми вершинами второй доли вершин.

Это дерево, подграф данного графа, с тем же числом вершин, что и у исходного графа. Неформально говоря, остовное дерево получается из исходного графа удалением максимального числа рёбер, входящих в циклы, но без нарушения связности графа. Остовное дерево включает в себя все n вершин исходного графа и содержит n - 1 ребро.