Минимальная Раскраска Графа (45 Фото)

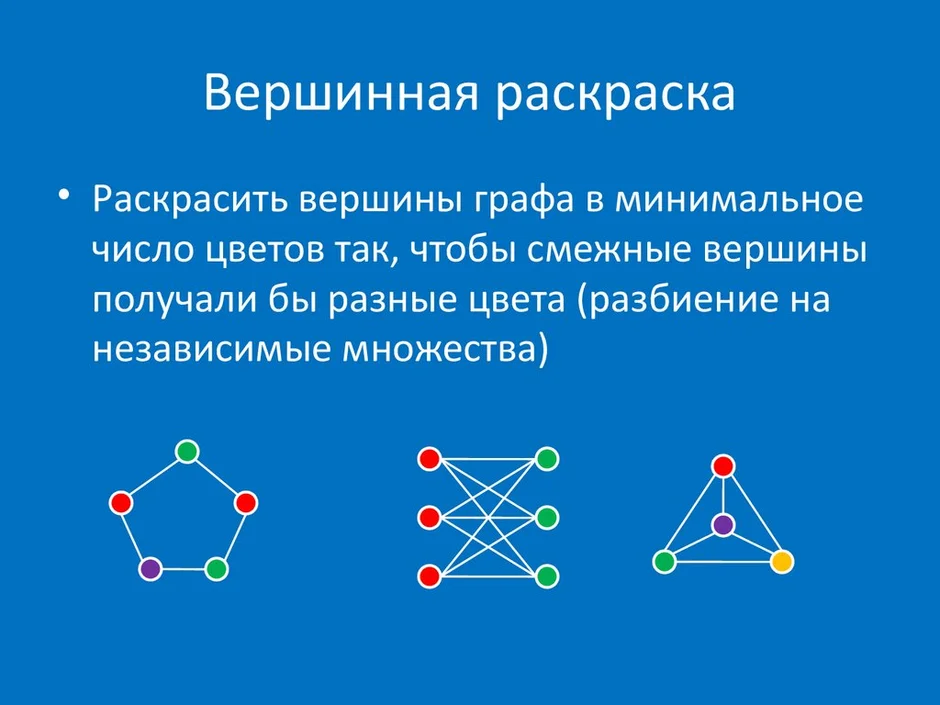
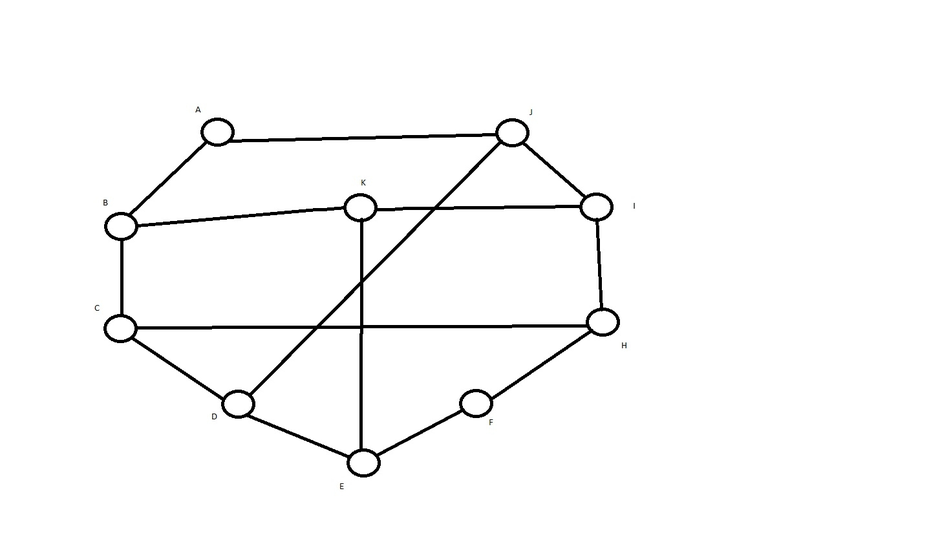
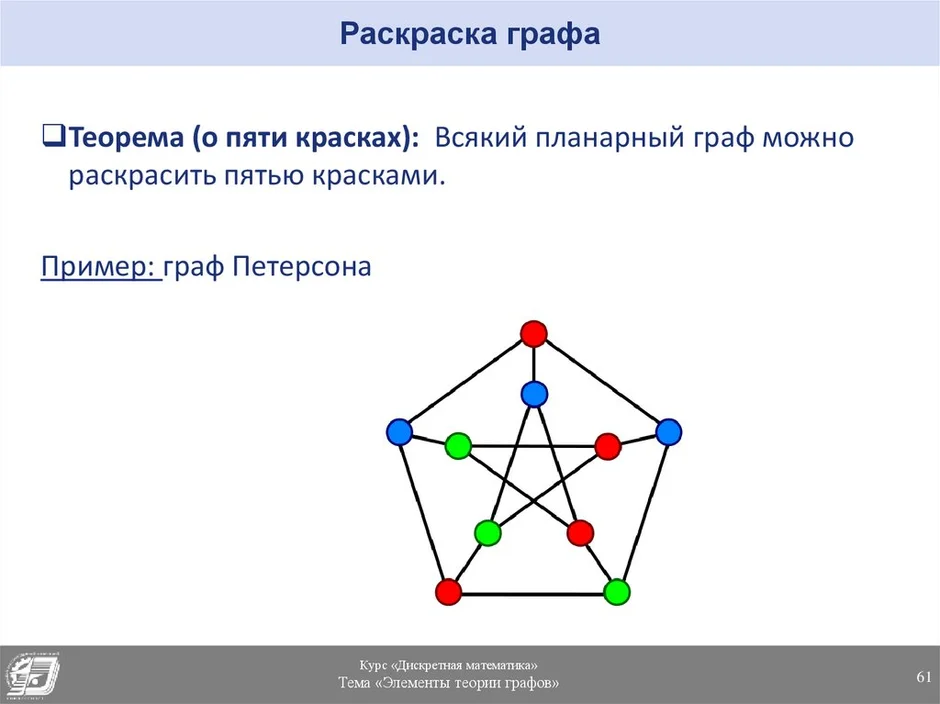
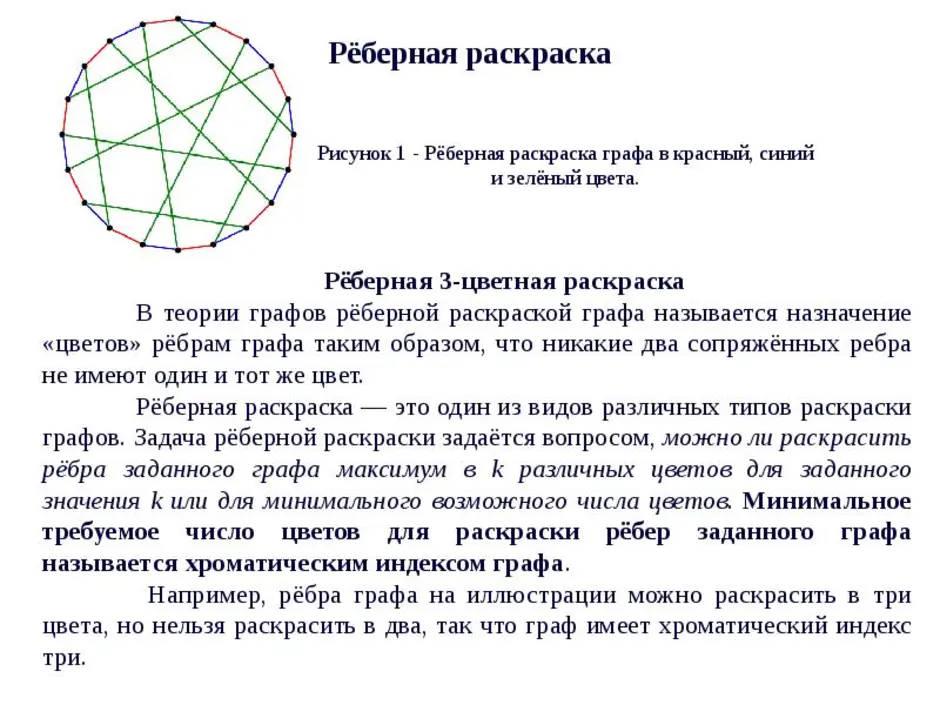
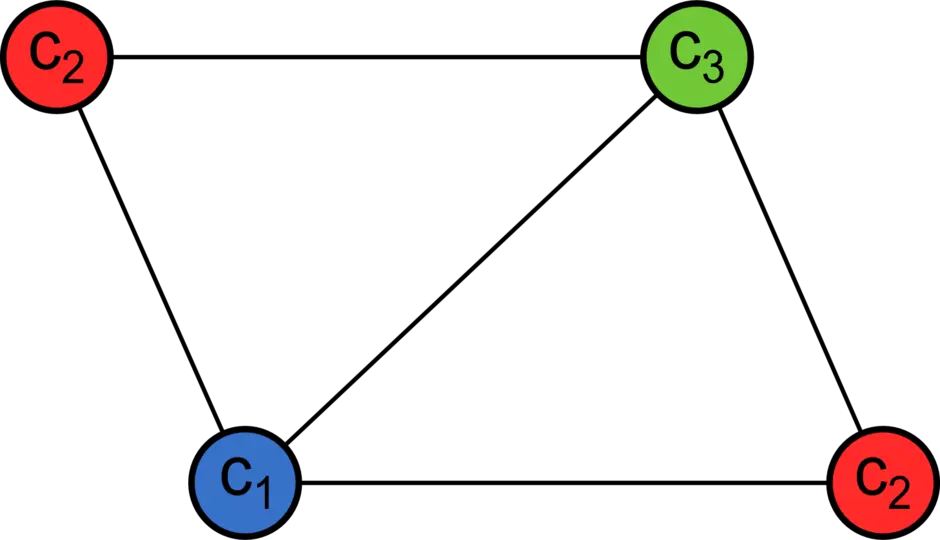
Теоретико-графовая конструкция, частный случай разметки графа. При раскраске элементам графа ставятся в соответствие метки с учётом определённых ограничений; эти метки традиционно называются «цветами». В простейшем случае такой способ окраски вершин графа, при котором любым двум смежным вершинам соответствуют разные цвета, называется раскраской вершин. Аналогично раскраска рёбер присваивает цвет каждому ребру так, чтобы любые два смежных ребра имели разные цвета. Наконец, раскраска областей планарного графа назначает цвет каждой области, так, что каждые две области, имеющие общую границу, не могут иметь одинаковый цвет.

Иерархическая структура данных, в которой каждый узел имеет не более двух потомков. Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками. Двоичное дерево является упорядоченным ориентированным деревом.

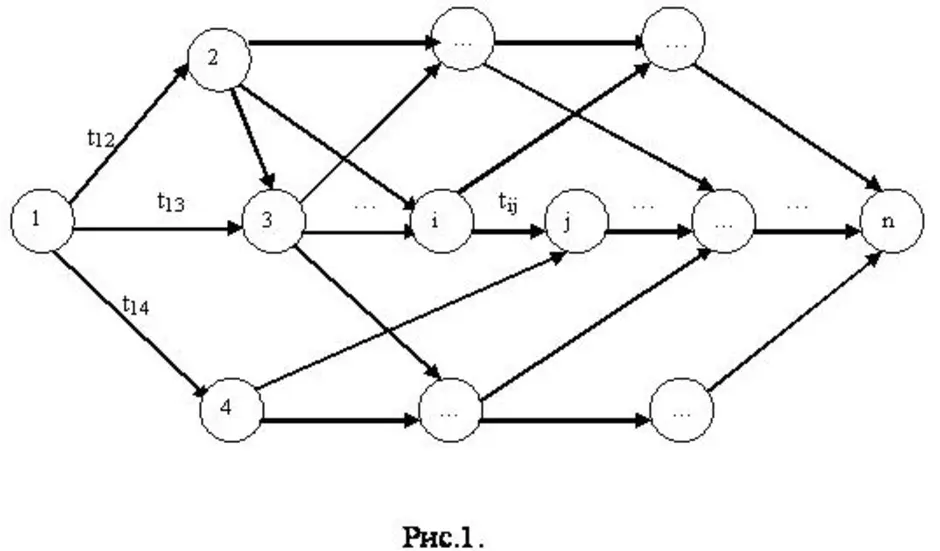
Граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами. Граф, ни одному ребру которого не присвоено направление, называется неориентированным графом или неорграфом.

Граф, который можно изобразить на плоскости без пересечений рёбер не по вершинам. Какое-либо конкретное изображение планарного графа на плоскости без пересечения рёбер не по вершинам называется плоским графом. Иначе говоря, планарный граф изоморфен некоторому плоскому графу, изображённому на плоскости так, что его вершины - это точки плоскости, а рёбра - кривые на плоскости, которые если и пересекаются между собой, то только по вершинам. Области, на которые граф разбивает плоскость, называются его гранями. Неограниченная часть плоскости - тоже грань, называемая внешней гранью. Любой плоский граф может быть спрямлён, то есть перерисован на плоскости так, что все его рёбра будут отрезками прямых.

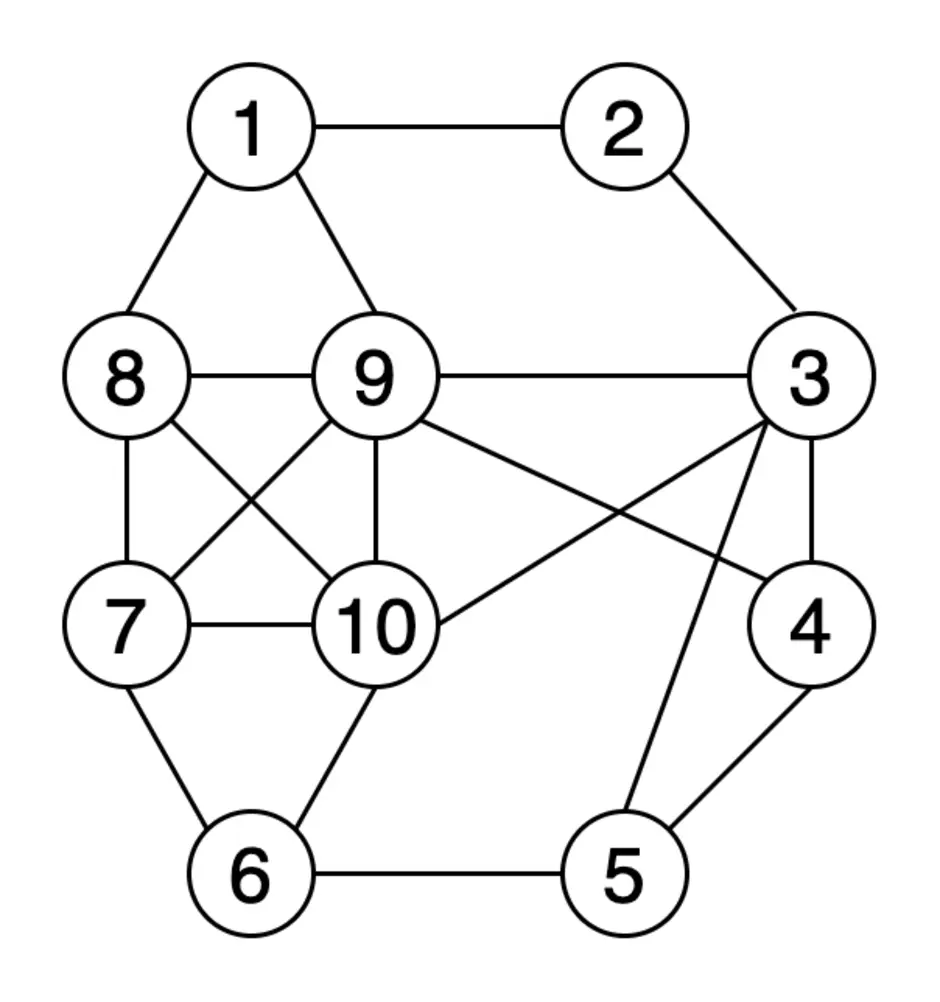
Это дерево, подграф данного графа, с тем же числом вершин, что и у исходного графа. Неформально говоря, остовное дерево получается из исходного графа удалением максимального числа рёбер, входящих в циклы, но без нарушения связности графа. Остовное дерево включает в себя все n вершин исходного графа и содержит n - 1 ребро.